Week 1
In this assignment, you will implement models that correct words that are 1 and 2 edit distances away.
- We say two words are n edit distance away from each other when we need n edits to change one word into another.
An edit could consist of one of the following options:
- Delete (remove a letter): ‘hat’ => ‘at, ha, ht’
- Switch (swap 2 adjacent letters): ‘eta’ => ‘eat, tea,…’
- Replace (change 1 letter to another): ‘jat’ => ‘hat, rat, cat, mat, …’
- Insert (add a letter): ‘te’ => ‘the, ten, ate, …’

Given the dictionary of word counts, compute the probability that each word will appear if randomly selected from the corpus of words.
\(P(w_i) = \frac{C(w_i)}{M} \tag{Eqn-2}\) where
$C(w_i)$ is the total number of times $w_i$ appears in the corpus.
$M$ is the total number of words in the corpus.
For example, the probability of the word ‘am’ in the sentence ‘I am happy because I am learning’ is:
\[P(am) = \frac{C(w_i)}{M} = \frac {2}{7} \tag{Eqn-3}.\]Python list comprehensions
character deleted.
For example, given the word nice, it would return the set: {‘ice’, ‘nce’, ‘nic’, ‘nie’}.

Step 1: Create a list of ‘splits’. This is all the ways you can split a word into Left and Right: For example,
‘nice is split into : [('', 'nice'), ('n', 'ice'), ('ni', 'ce'), ('nic', 'e'), ('nice', '')]
This is common to all four functions (delete, replace, switch, insert).

Step 2: This is specific to delete_letter. Here, we are generating all words that result from deleting one character.
This can be done in a single line with a list comprehension. You can make use of this type of syntax:
[f(a,b) for a, b in splits if condition]
For our ‘nice’ example you get: [‘ice’, ‘nce’, ‘nie’, ‘nic’]

Short circuit
In Python, logical operations such as and and or have two useful properties. They can operate on lists and they have ‘short-circuit’ behavior. Try these:
# example of logical operation on lists or sets
print( [] and ["a","b"] )
print( [] or ["a","b"] )
#example of Short circuit behavior
val1 = ["Most","Likely"] or ["Less","so"] or ["least","of","all"] # selects first, does not evalute remainder
print(val1)
val2 = [] or [] or ["least","of","all"] # continues evaluation until there is a non-empty list
print(val2)
- Sets have a handy set.intersection feature
- To find the keys that have the highest values in a dictionary, you can use the Counter dictionary to create a Counter object from a regular dictionary. Then you can use Counter.most_common(n) to get the n most common keys.
- To find the intersection of two sets, you can use set.intersection or the & operator.
Dynamic Programming
he diagram below describes how to initialize the table. Each entry in D[i,j] represents the minimum cost of converting string source[0:i] to string target[0:j]. The first column is initialized to represent the cumulative cost of deleting the source characters to convert string “EER” to “”. The first row is initialized to represent the cumulative cost of inserting the target characters to convert from “” to “NEAR”.
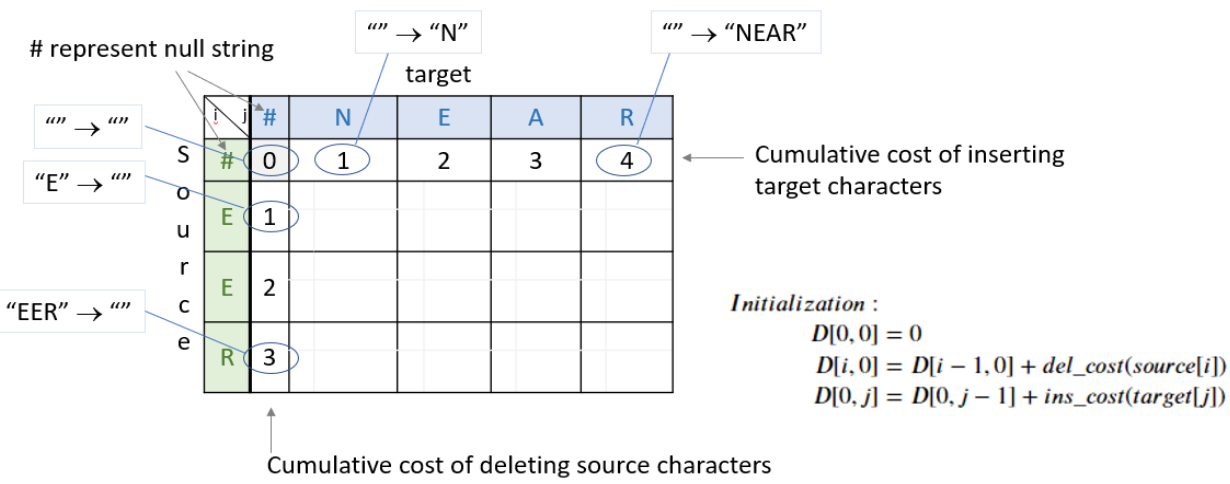
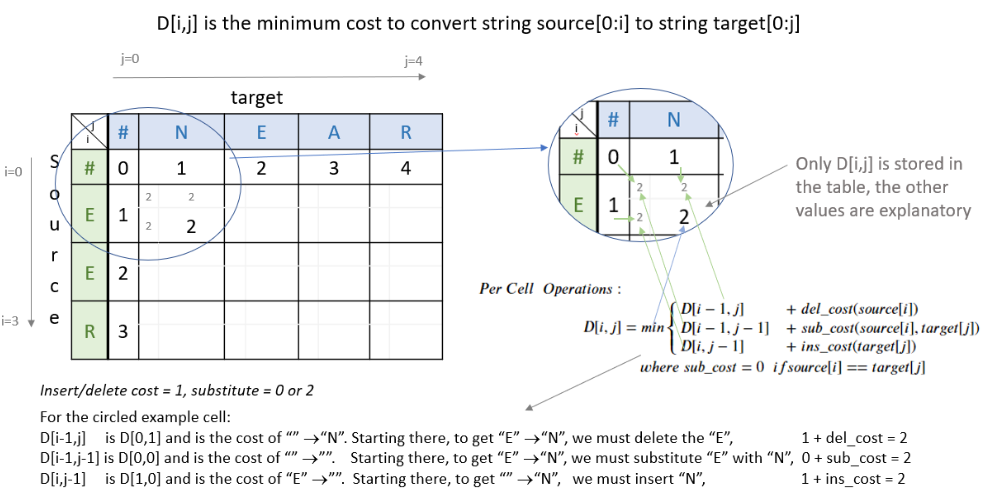
Filling in the remainder of the table utilizes the ‘Per Cell Operations’ in the equation (5) above. Note, the diagram below includes in the table some of the 3 sub-calculations shown in light grey. Only ‘min’ of those operations is stored in the table in the min_edit_distance() function.
Week 2 : Part of Speech taggin
The smoothing was done as follows:
\[P(t_i | t_{i-1}) = \frac{C(t_{i-1}, t_{i}) + \alpha }{C(t_{i-1}) +\alpha * N}\tag{3}\]- $N$ is the total number of tags
- $C(t_{i-1}, t_{i})$ is the count of the tuple (previous POS, current POS) in
transition_countsdictionary. - $C(t_{i-1})$ is the count of the previous POS in the
tag_countsdictionary. - $\alpha$ is a smoothing parameter.
Exercise 6 - initialize
Instructions:
Write a program below that initializes the best_probs and the best_paths matrix.
Both matrices will be initialized to zero except for column zero of best_probs.
- Column zero of
best_probsis initialized with the assumption that the first word of the corpus was preceded by a start token (“–s–”). - This allows you to reference the A matrix for the transition probability
Here is how to initialize column 0 of best_probs:
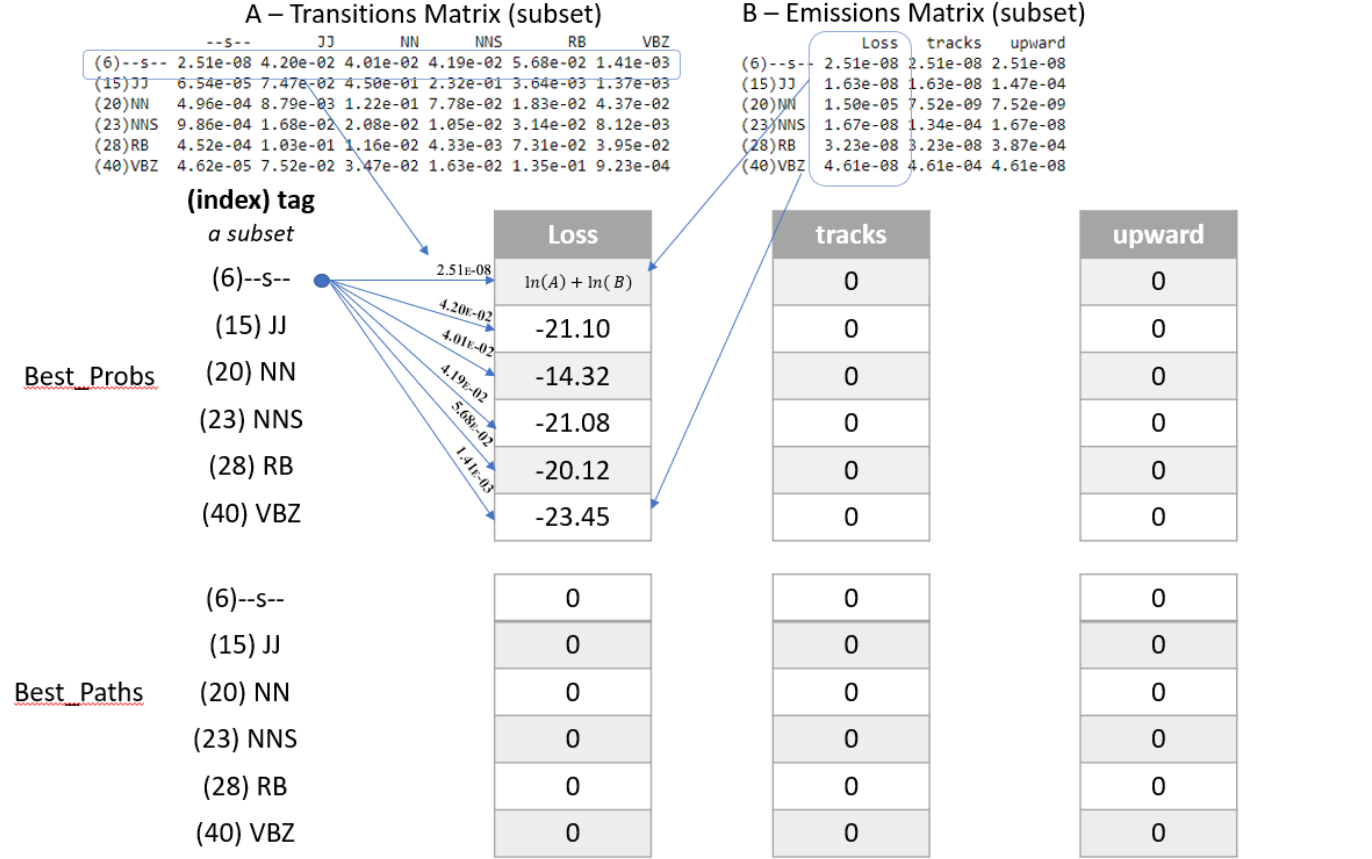
- The probability of the best path going from the start index to a given POS tag indexed by integer $i$ is denoted by ${best_probs}[s_{idx}, i]$.
- This is estimated as the probability that the start tag transitions to the POS denoted by index $i$: $\mathbf{A}[s_{idx}, i]$ AND that the POS tag denoted by $i$ emits the first word of the given corpus, which is $\mathbf{B}[i, vocab[corpus[0]]]$.
- Note that vocab[corpus[0]] refers to the first word of the corpus (the word at position 0 of the corpus).
- vocab is a dictionary that returns the unique integer that refers to that particular word.
Conceptually, it looks like this: ${best_probs}[s_{idx}, i] = \mathbf{A}[s_{idx}, i] \times \mathbf{B}[i, corpus[0] ]$
In order to avoid multiplying and storing small values on the computer, we’ll take the log of the product, which becomes the sum of two logs:
$best_probs[i,0] = log(A[s_{idx}, i]) + log(B[i, vocab[corpus[0]]$
Also, to avoid taking the log of 0 (which is defined as negative infinity), the code itself will just set $best_probs[i,0] = float(‘-inf’)$ when $A[s_{idx}, i] == 0$
So the implementation to initialize $best_probs$ looks like this:
${if}\ A[s_{idx}, i] <> 0 : best_probs[i,0] = log(A[s_{idx}, i]) + log(B[i, vocab[corpus[0]]])$
${if}\ A[s_{idx}, i] == 0 : best_probs[i,0] = float(‘-inf’)$
3.2 - Viterbi Forward
In this part of the assignment, you will implement the viterbi_forward segment. In other words, you will populate your best_probs and best_paths matrices.
- Walk forward through the corpus.
- For each word, compute a probability for each possible tag.
- Unlike the previous algorithm
predict_pos(the ‘warm-up’ exercise), this will include the path up to that (word,tag) combination.
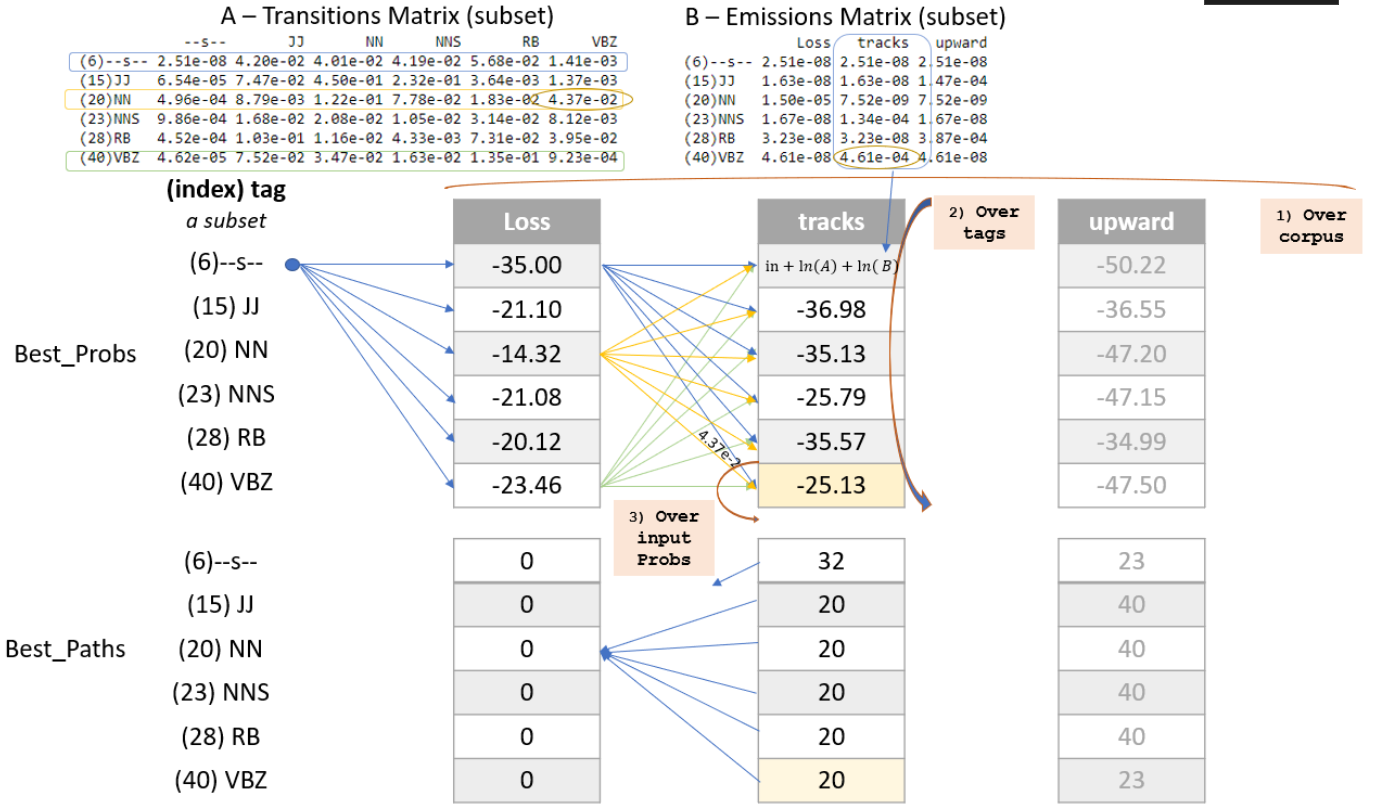
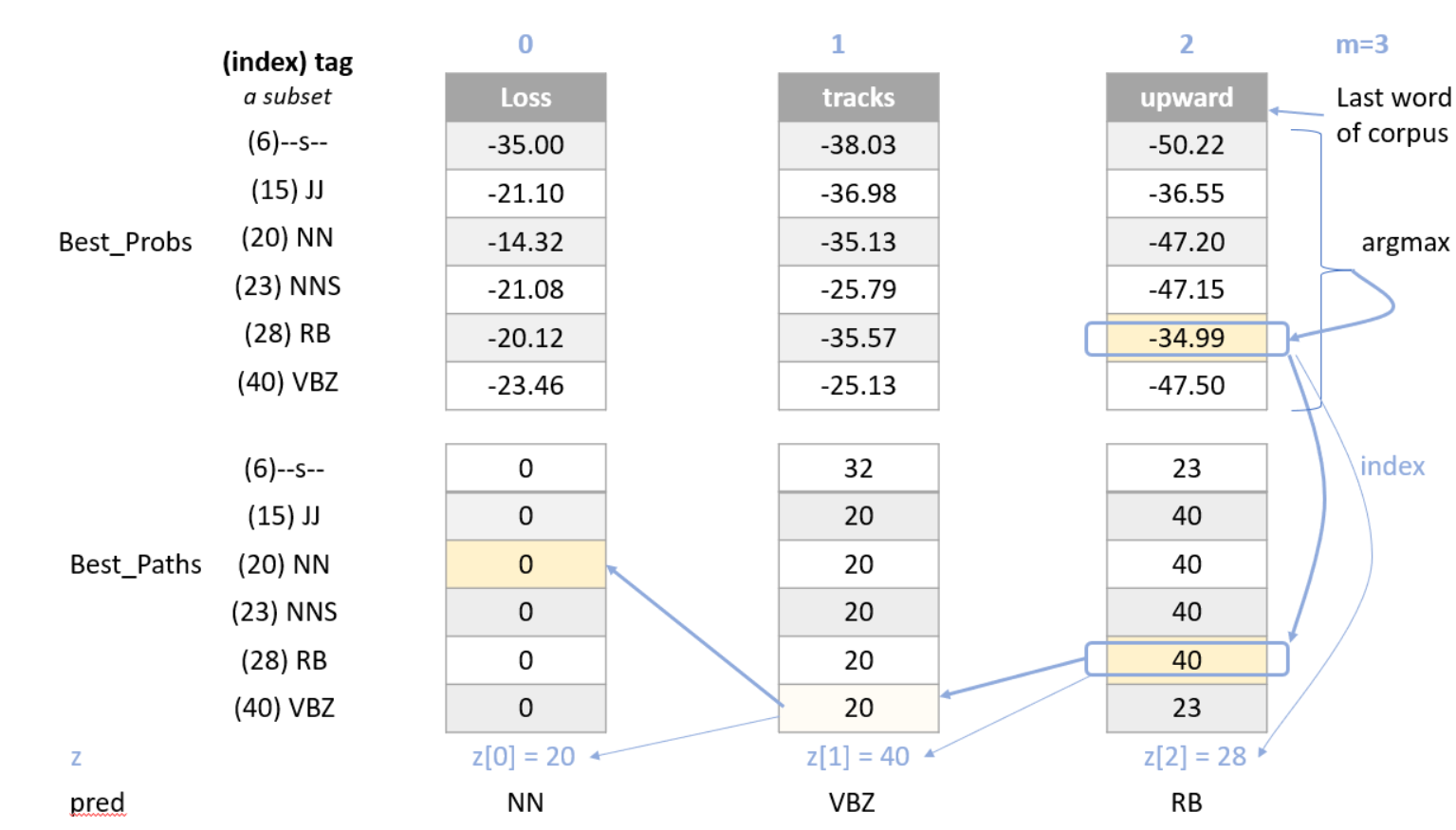
Here is an example with a three-word corpus “Loss tracks upward”:
- Note, in this example, only a subset of states (POS tags) are shown in the diagram below, for easier reading.
- In the diagram below, the first word “Loss” is already initialized.
- The algorithm will compute a probability for each of the potential tags in the second and future words.
Compute the probability that the tag of the second word (‘tracks’) is a verb, 3rd person singular present (VBZ).
- In the
best_probsmatrix, go to the column of the second word (‘tracks’), and row 40 (VBZ), this cell is highlighted in light orange in the diagram below. - Examine each of the paths from the tags of the first word (‘Loss’) and choose the most likely path.
- An example of the calculation for one of those paths is the path from (‘Loss’, NN) to (‘tracks’, VBZ).
- The log of the probability of the path up to and including the first word ‘Loss’ having POS tag NN is $-14.32$. The
best_probsmatrix contains this value -14.32 in the column for ‘Loss’ and row for ‘NN’. - Find the probability that NN transitions to VBZ. To find this probability, go to the
Atransition matrix, and go to the row for ‘NN’ and the column for ‘VBZ’. The value is $4.37e-02$, which is circled in the diagram, so add $-14.32 + log(4.37e-02)$. - Find the log of the probability that the tag VBS would ‘emit’ the word ‘tracks’. To find this, look at the ‘B’ emission matrix in row ‘VBZ’ and the column for the word ‘tracks’. The value $4.61e-04$ is circled in the diagram below. So add $-14.32 + log(4.37e-02) + log(4.61e-04)$.
- The sum of $-14.32 + log(4.37e-02) + log(4.61e-04)$ is $-25.13$. Store $-25.13$ in the
best_probsmatrix at row ‘VBZ’ and column ‘tracks’ (as seen in the cell that is highlighted in light orange in the diagram). - All other paths in best_probs are calculated. Notice that $-25.13$ is greater than all of the other values in column ‘tracks’ of matrix
best_probs, and so the most likely path to ‘VBZ’ is from ‘NN’. ‘NN’ is in row 20 of thebest_probsmatrix, so $20$ is the most likely path. - Store the most likely path $20$ in the
best_pathstable. This is highlighted in light orange in the diagram below.
for each word in the corpus
for each POS tag type that this word may be
for POS tag type that the previous word could be
compute the probability that the previous word had a given POS tag, that the current word has a given POS tag, and that the POS tag would emit this current word.
retain the highest probability computed for the current word
set best_probs to this highest probability
set best_paths to the index 'k', representing the POS tag of the previous word which produced the highest probability
3.3 - Viterbi Backward
Now you will implement the Viterbi backward algorithm.
- The Viterbi backward algorithm gets the predictions of the POS tags for each word in the corpus using the
best_pathsand thebest_probsmatrices.
The example below shows how to walk backwards through the best_paths matrix to get the POS tags of each word in the corpus. Recall that this example corpus has three words: “Loss tracks upward”.
POS tag for ‘upward’ is RB
- Select the the most likely POS tag for the last word in the corpus, ‘upward’ in the
best_probtable. - Look for the row in the column for ‘upward’ that has the largest probability.
- Notice that in row 28 of
best_probs, the estimated probability is -34.99, which is larger than the other values in the column. So the most likely POS tag for ‘upward’ isRBan adverb, at row 28 ofbest_prob. - The variable
zis an array that stores the unique integer ID of the predicted POS tags for each word in the corpus. In array z, at position 2, store the value 28 to indicate that the word ‘upward’ (at index 2 in the corpus), most likely has the POS tag associated with unique ID 28 (which isRB). - The variable
predcontains the POS tags in string form. Sopredat index 2 stores the stringRB.
POS tag for ‘tracks’ is VBZ
- The next step is to go backward one word in the corpus (‘tracks’). Since the most likely POS tag for ‘upward’ is
RB, which is uniquely identified by integer ID 28, go to thebest_pathsmatrix in column 2, row 28. The value stored inbest_paths, column 2, row 28 indicates the unique ID of the POS tag of the previous word. In this case, the value stored here is 40, which is the unique ID for POS tagVBZ(verb, 3rd person singular present). - So the previous word at index 1 of the corpus (‘tracks’), most likely has the POS tag with unique ID 40, which is
VBZ. - In array
z, store the value 40 at position 1, and for arraypred, store the stringVBZto indicate that the word ‘tracks’ most likely has POS tagVBZ.
POS tag for ‘Loss’ is NN
- In
best_pathsat column 1, the unique ID stored at row 40 is 20. 20 is the unique ID for POS tagNN. - In array
zat position 0, store 20. In arraypredat position 0, storeNN.
Course 3 Language Models and Auto-Complete
Develop n-gram based Language Models
In this section, you will develop the n-grams language model.
- Assume the probability of the next word depends only on the previous n-gram.
- The previous n-gram is the series of the previous ‘n’ words.
The conditional probability for the word at position ‘t’ in the sentence, given that the words preceding it are $w_{t-n}\cdots w_{t-2}, w_{t-1}$ is:
\[P(w_t | w_{t-n}\dots w_{t-1} ) \tag{1}\]You can estimate this probability by counting the occurrences of these series of words in the training data.
- The probability can be estimated as a ratio, where
- The numerator is the number of times word ‘t’ appears after words t-n through t-1 appear in the training data.
- The denominator is the number of times word t-n through t-1 appears in the training data.
- The function $C(\cdots)$ denotes the number of occurence of the given sequence.
- $\hat{P}$ means the estimation of $P$.
- Notice that denominator of the equation (2) is the number of occurence of the previous $n$ words, and the numerator is the same sequence followed by the word $w_t$.
Later, you will modify the equation (2) by adding k-smoothing, which avoids errors when any counts are zero.
The equation (2) tells us that to estimate probabilities based on n-grams, you need the counts of n-grams (for denominator) and (n+1)-grams (for numerator).